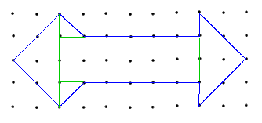
For the problem on the previous page we can decompose the figure as in the diagram with two triangles of area 4 at the ends, two triangles of area 1/2 each and one large rectangle of area 16 giving a total of 21.
For the problem on the previous page we can decompose the figure as in the diagram with two triangles of area 4 at the ends, two triangles of area 1/2 each and one large rectangle of area 16 giving a total of 21.
However sometimes the decomposition method does not work on dot figures. For example, consider the triangle ABC below where none of the sides can be used as the base, since there is no horizontal or vertical side.
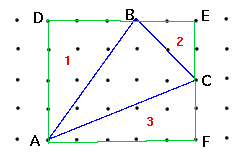But we can enclose our triangle in the rectangle ADEF which has area 4*5 = 20. We then subtract the areas of triangle 1 which has base 4 height 3 and area 6, triangle 2 of base and height 2 and area 2, and triangle 3 with base 5, height 2 and area 5. The total area of these three triangles is 13, subtracting 13 from 20 leaves 7, the area of triangle ABC.
This method, which can be used for other figures as well, does work for all triangles. It is not hard to see that any dot figure can be broken into triangles as long as we don't require that they have a horizontal or vertical side, hence we can now calculate the areas of all dot figures. Moreover, a dot triangle will have either a whole number or half of a whole number as area, so this also will be true of all dot figures.
Try to find the area of the following parallelogram, but be careful since there is no horizontal or vertical side.
