Pick's Theorem -- Page 6
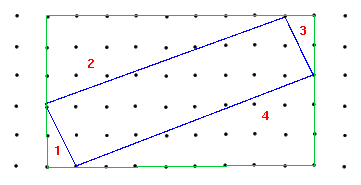 The parallelogram of the previous question is enclosed in a rectangle of base 9 and height 5 so area 45. But triangles 1,3 have area 1 while triangles 2,4 have base 8 and height 3 and area 12. So the area of the parallelogram is 45 - 2(1) - 2(12) = 19.
The parallelogram of the previous question is enclosed in a rectangle of base 9 and height 5 so area 45. But triangles 1,3 have area 1 while triangles 2,4 have base 8 and height 3 and area 12. So the area of the parallelogram is 45 - 2(1) - 2(12) = 19.
One must be careful here. One might think this is a rectangle. Using the Pythagorean theorem one can easily calculate the long side by 4 as the square root of 73, that is about 8.5440. The short side by 3 is the square root of 5, about 2.2361. Multiplying we would get the area of the rectangle as 19.1051 but this is wrong. All dot figures have areas that are integers or halves of integers as we have seen. So this is figure is not quite a rectangle.
Now that we know how to find areas of dot figures I will help you discover a shortcut.
Each dot figure is a polygon and hence has an "inside" and "outside". Dots in the inside of the figure are called interior dots while points on the outside are called exterior dots. The dots that are on the figure are called boundary dots.
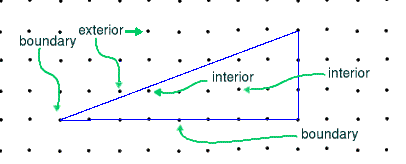
Of course there are infinitely many exterior points so those are not interesting. Over the next several pages we will tabulate the number of boundary dots, interior dots and the area of the figures below to see if there is a pattern.
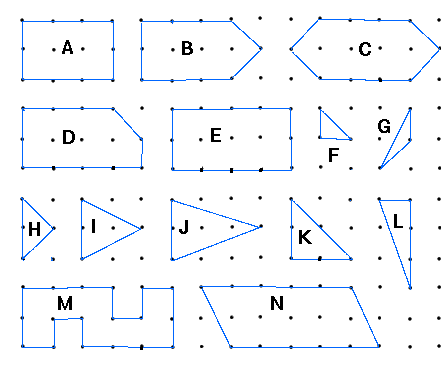
| Figure | A | B | C | D | E | F | G | H | I | J | K | L | M | N |
|---|
boundary
dots | 10 | 10 | 10 | 11 | 12 | 3 | | 4 | 4 | 4 | 6 | | | 12 |
|---|
interior
dots | 2 | 3 | 4 | ? | 3 | ? | 0 | 0 | 1 | | | 0 | 0 | 5 |
|---|
| Area | 6 | 7 | ? | ? | ? | | | | | | | | | |
|---|
CONTINUE
 The parallelogram of the previous question is enclosed in a rectangle of base 9 and height 5 so area 45. But triangles 1,3 have area 1 while triangles 2,4 have base 8 and height 3 and area 12. So the area of the parallelogram is 45 - 2(1) - 2(12) = 19.
The parallelogram of the previous question is enclosed in a rectangle of base 9 and height 5 so area 45. But triangles 1,3 have area 1 while triangles 2,4 have base 8 and height 3 and area 12. So the area of the parallelogram is 45 - 2(1) - 2(12) = 19.

