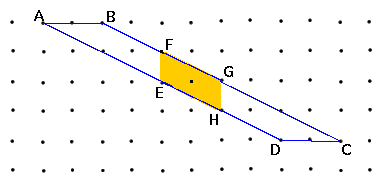
The answer to the last question is that the big parallelogram has area 8 (base 2, height 4) and the small one has area 2 (base 1 height 2). Without actually calculating the small parallelogram seems like more than 1/4 of the large one.
BACK
We can also find the area of more complicated regions by breaking them up into simple regions. In the picture below we show how to break up some complicated regions.
For drawing A we have the square 1 with area 4 and the triangle 2 with area 2 for a total area of 6. Octogon B consists of 4 triangles 1 of area 1/2 for a total of 2, two squares 2 of area 1 each and the one rectangle 3 of area 3 for a total of 7. Figure C has two triangles 1 of area 1, two triangles 2 of area 1/2, a rectangle 3 of area 2 and another rectangle 4 of area 4. The total area of C is thus 9. Figure D has a rectangle 1 of area 6, triangles 2,3 of areas 1/2 and 1 and three squares 4 of area 1 for a total of 10 1/2. Finally kite E consists of two triangles 1,2 of areas 2 and 4 respectively for a total area of 6. There are many other ways to decompose this kite.
Now you calculate the area of the following dot figure.
CONTINUE
