Pick's Theorem -- Page 15

The most accessable "proof" of Pick's theorem involves 5 steps.

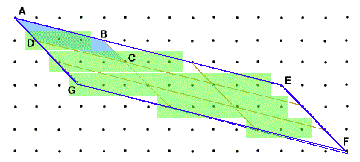Step 1: Pick's theorem is proven for the general parallelogram. This is suprisingly hard. The proof goes something like this. Tile a large area with copies of the original parallelogram (ABCD in the picture) to get a large parallelogram (AEFG in the picture). Now approximate the area of the large by rectangular regions centered(the yellow regions in the picture) centered around the interior and half minus one of the boundary dots (yellow portion of picture, here 27). It turns out that the error becomes small relative to the number of tiles. Dividing by the number of tiles (here 9) one shows, with some difficulty, that the approximation B/2 + I - 1 of the area of the original parallelogram is good to less than one unit if we have enough tiles. But since we know that the area of a dot parallelogram must be an integer the approximate answer must be exact.

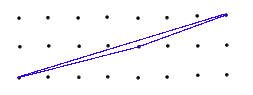Step 2: We really only need the result above when the parallelogram above has 4 boundary dots and no interior dots, but that case wouldn't have been any easier. Any triangle with only three boundary dots and no interior dots can be rotated along the center of one side to produce such a parallelogram. Hence any triangle with B=3 and I=0 has area 1/2 as predicted by Pick's Theorem. (You might want to verify the answer with this example by enclosing the triangle in a big rectangle of area 14 and subtracting off the portion not in the triangle.)

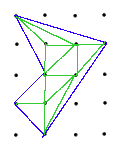Step 3:We now triangulate our dot figure, that is, break it up into triangles. Unlike early in this worksheet the sides need not be horizontal or vertical so this can always be done. Also, as seen in the picture, if a triangle has at least one boundary dot which is not a vertex, or has an interior dot, then it can be further subdivided. Thus we can divide up our figure into dot triangles with B=3 and I=0. Since we know each triangle has area 1/2 it remains to count up these triangles.

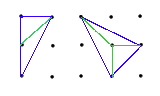Step 4:We now view our triangulated dot figure as a network, that is, composed of vertices, edges and regions. The number of vertices is clearly V = B+I. It is somewhat harder to count edges, but each additonal interior point produces 3 new edges and each new boundary dot produces 2 new edges (one to a different vertex and one because an existing edge is broken into two). However, since the minimim dot figure has B=3 and I=0 and only 3 edges the formula is

E = 3I + 2B -3 One can check on the example on the above right which has B=5, I=4, V=9 and E = 3(4) + 2(5) - 3 = 19. (Don't forget to count the blue edges on the original boundary).

Step 5: We now count regions by Euler's formula: R + V = E + 2, or R = E - V + 2. But using our count of vertices and edges from step 4 we get

R = (3I + 2B -3) - (B + I) + 2 = 2I + B -1 But remember that Euler's formula includes the "outside" region leaving R - 1 triangles each of area 1/2. So the area is Area = ¹/₂(R - 1) = ¹/₂((2I+B-1) - 1) = ¹/₂(2I - B - 2) = I + ^B/₂ - 1 which is Pick's formula.

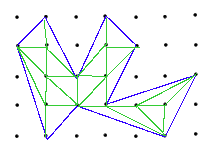The last five questions refer to the dot figure on the right.

The correct answers are that there are 7 interior dots, 10 boundary dots, 38 edges. The area of the figure is 11 and all of the equations are true.

Goodbye, hope you had fun.